trabajo N 2 : funciones
➤¿QUÉ ES UNA FUNCIÓN LINEAL?
Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
Una función lineal es lineal cuando su gráfica es una recta .
La función lineal se define por la ecuación f(x) = x + b ó y = x + b esa ecuación es llamada ecuación canónica , (x) es la pendiente de la recta y (b) es el intercepto con el eje (y).El numero x se llama pendiente de la recta y es la relación entre la altura y la base de la recta
foto de ejemplo:
video de explicación:
pag donde busque ejemplos y información:
http://matefacil01.blogspot.com.ar/2011/05/funcion-lineal.html
➤ ¿QUÉ ES LA ORDENADA AL ORIGEN?
La ordenada al origen te indica la posición en el eje "X" , y donde la recta corta en el eje "Y".
La ordenada al origen es le punto de intersección de la recta con el eje "y" . En la ecuación cartesiana , que tiene forma ejemplo: y=mx+b , la ordenada al origen es b.
El punto de intersección de la recta con el eje "x" se denomina ABSCISA AL ORIGEN , el número que acompaña a la "x" en la ecuación cartesiana se llama PENDIENTE de la recta y es la tangente trígonométrica
del angulo de inclinación.
Es la forma pendiente al origen de las ecuaciones de dos variables, es una representación especifica de las ecuaciones lineales . La forma pendiente - ordenada al origen tiene la ventaja de que exhibe las dos características principales de la recta que representa .
VIDEO DE EXPLICACIÓN:⇳⇳
¿CUÁL ES EL MODELO DE UNA FUNCIÓN CUADRÁTICA?
En matemáticas, una función cuadrática o función de segundo grado es una función polinómica de grado dos definida como
•en donde a, b y c son números reales (constantes) y a es distinto de 0.
Una función cuadrática es una función que puede ser descrita por una ecuación de la forma y = ax2 + bx + c, donde a ≠ 0. Ningún término en la función polinomial tiene un grado mayor que 2. Las funciones cuadráticas son útiles cuando trabajamos con áreas, y frecuentemente aparecen en problemas de movimiento que implican gravedad o aceleración.
Las gráficas de las funciones cuadráticas tienen características que están relacionadas con su forma simbólica. A medida que exploremos estas gráficas, aprenderemos a identificar estas características, y veremos algunas de las maneras de estructurar las ecuaciones cuadráticas.
Una función cuadrática es un polinomio de grado 2, el exponente más alto en la variable es 2. Los ejemplos son de funciones cuadráticas:
La función cuadrática más básica y simple tiene la ecuación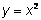 
. Si en una tabla hacemos con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática.
. Si en una tabla hacemos con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática.
La forma estándar de una ecuación cuadrática es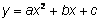 
. ejemplo , el valor del coeficiente a es 1, y b y c son 0. Si bien muchas ecuaciones cuadráticas presentan valores de b y c diferentes de cero, la gráfica resultante siempre será una parábola.
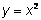. ejemplo , el valor del coeficiente a es 1, y b y c son 0. Si bien muchas ecuaciones cuadráticas presentan valores de b y c diferentes de cero, la gráfica resultante siempre será una parábola.
Las parábolas tienen muchas propiedades que pueden ayudarnos a graficar ecuaciones cuadráticas. Una parábola tiene un punto especial llamado vértice; este es el punto donde la U "da la vuelta". Nota que en el vértice, la parábola cambia de dirección: ejemplo de imagen
vértice: es el punto donde la parábola alcanza su máximo o su mínimo.
Con esta ecuación se obtiene el vértice:
EL EJE DE SIMETRÍA:
La recta vertical que parte la parábola en dos mitades simétricas y pasa por el vértice.
ejemplo: y = x2 – 2x -3 es
Para una función cuadrática y = ax2 + bx + c, la coordenada x del vértice es siempre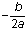 
. Como el eje de simetría siempre pasa por el vértice, significa que el eje de simetría es una línea vertical 
. Cambia los valores de a y b en la gráfica siguiente para ver dónde están el vértice y la línea de simetría.
. Como el eje de simetría siempre pasa por el vértice, significa que el eje de simetría es una línea vertical 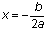. Cambia los valores de a y b en la gráfica siguiente para ver dónde están el vértice y la línea de simetría.
RAÍCES:
Las raíces son los puntos donde la parábola corta con el eje horizontal.
Una parábola puede tener 2 raíces, una raíz o ninguna, la función puede cortar en el eje X en dos puntos , un punto o ninguno.
ejemplo en esta imagen:
INTERCEPCIONES:
Puede encontrar la intercepción en Y de una parábola simplemente al introducir 0 para X . Si la ecuación esta en la forma estándar, entonces solo toma a C como la intercepción en Y .
Las intercepciones en X son un poco más complicadas. Puede usar la factorización , o completar el cuadrado , o la formula cuadrática para encontrar estas.
DOMINIO Y RANGO:
Como con cualquier función, el dominio de función cuadrática F ( X) es el conjunto de los valores de X para los cuales la función esta definida, y el rango es el conjunto de todos los valores de salida (valores de F).
Las funciones cuadráticas generalmente tienen la recta real de enteros como su dominio: cualquier X es una entrada legítima. El rango esta restringido a esos puntos mayores que o iguales a la coordenada en y del vértice (o menores que o iguales a, dependiendo si la parábola abre hacia arriba o hacia abajo).
Se llama imagen al recorrido de una función y se designa im f, a todos los valores de la variable dependiente que tienen algún valor de la variable independiente que se transforma en el por la función
Comentarios
Publicar un comentario